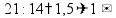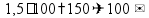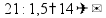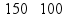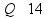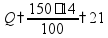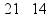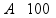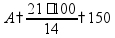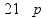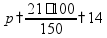Действия в столбик
|
Сложение «в столбик» Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху более длинное число - так удобней).
Складываем по одной цифре справа налево, результат записываем под чертой.
Если получится число > 10, записываем только последнюю цифру результата, а первую цифру ставим пока над соседней цифрой слева (для сложения на следующем шаге).
|
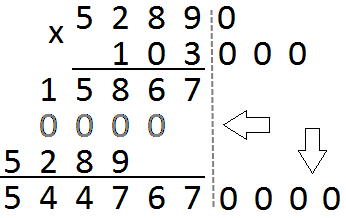
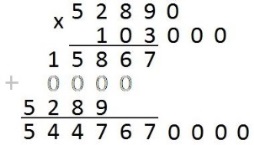
Умножение «в столбик» Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху более длинное число - так удобней).
Сначала умножаем верхнее число на последнюю цифру нижнего числа. Результат записываем под чертой.
Переходим к умножению на следующую цифру второго числа. Результат умножения на следующую цифру записывается со сдвигом.
Если во втором числе есть нули, то получится «нулевая строчка» - ее можно не писать, но тогда нужно будет сделать сдвиг на две клетки. При умножении чисел, оканчивающихся нулями, нужно сначала «отделить» нули - записать и умножить числа без последних нулей, потом все нули добавить к результату.
|
|||||||||||||||||||||||||||||||||||||||
|
Вычитание «в столбик» Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху уменьшаемое, снизу вычитаемое).
Выполняем вычитание по одной цифре справа налево, результат записываем под чертой.
Если сверху окажется меньшая цифра, то нужно «занять десяток» из соседней цифры слева (над соседней цифрой ставим точку).
|
||||||||||||||||||||||||||||||||||||||||
|
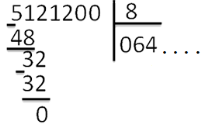
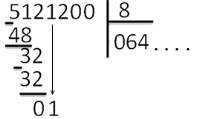
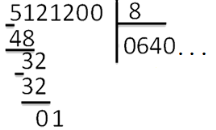
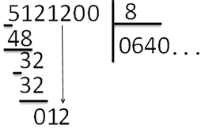
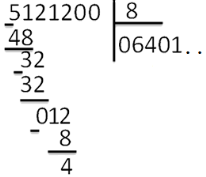
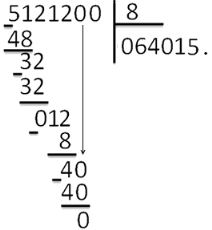
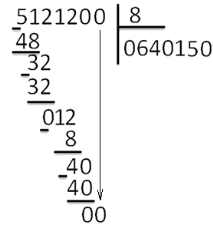
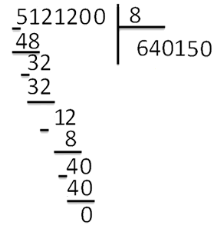
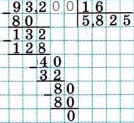
Деление «в столбик» Запишем делимое и делитель «в столбик». Результат (частное) будем записывать в «уголке» под делителем.
Чтобы избежать ошибок (связанных с пропуском нулей в результате), можно заранее поставить на место результата столько точек, сколько цифр в делимом. А при выполнении деления следить за тем, чтобы для каждой из цифр делимого была записана какая-то цифра в результат.
Будем делить не все делимое сразу, а «по частям». Для объяснения этих действий используется понятие «неполное частное» - это та часть делимого, с которой в данный момент работают. Сначала берем первую цифру делимого - принимаем ее за «неполное частное». Далее действуем по алгоритму:
«Обратно» умножаем делитель на полученную цифру результата, произведение записываем ниже делимого (для вычитания), вычитаем и получаем остаток. Остаток должен быть меньше делителя! Принимаем остаток за «неполное частное».
|
|
|||||||||||||||||||||||||||||||||||||||
Математика - 4 класс
|
Таблица умножения
|
Арифметические действия
|
|||||||
|
Простые уравнения Уравнение - это равенство, содержащее неизвестную величину (ее значение надо найти)
|
||||||||
|
Длина 1 км = 1000 м 1 м = 100 см 1 дм = 10 см 1 см = 10 мм Периметр
Площадь
|
Запись натуральных чисел _ _ _ _ _ _ _ _ _ _ _ _ млрд млн тыс едн (по три цифры в каждом классе) пр: 2 000 040 300 (два миллиарда сорок тысяч триста) |
|||||||
|
Римская система записи чисел
|
||||||||
|
Масса 1 т = 1000 кг 1 кг = 1000 г
|
Время 1
год
1
сут
1 ч = 60 мин 1 мин = 60 с високосные года (+29.02)
|
|||||||
|
Примеры действий в столбик
|
||||||||
|
Скорость
(S - путь, v - скорость, t - время) |
||||||||
Математика - 5 класс
|
Законы арифметики переместительный
сочетательный
распределительный
пр:
раскрытие скобок
пр:
вынесение общего множителя за скобки
вычитание суммы и разности
|
Длина 1 км = 1000 м 1 м = 100 см = 1000 мм 1 дм = 10 см = 100 мм 1 см = 10 мм Периметр (длина по границе фигуры)
Площадь (мера плоской фигуры)
Объем (мера пространства)
|
Скорость
(S - путь, v - скорость, t - время) Движение двух объектов в разных направлениях:
в одном направлении:
Движение по воде
|
||||||||||||||||||||||||||||||||||||||||
|
Порядок действий слева направо
4. сложение, вычитание |
обозначение единиц измерения (приставки СИ)
|
|||||||||||||||||||||||||||||||||||||||||
|
умножение
степень «a в степени n»
«a
в квадрате»
«a
в кубе»
пр:
|
||||||||||||||||||||||||||||||||||||||||||
|
углы
|
||||||||||||||||||||||||||||||||||||||||||
|
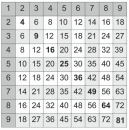
Таблица простых чисел простое число - делится только на 1 и само себя (1 «не считается» простым числом) 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 ... |
||||||||||||||||||||||||||||||||||||||||||
|
Делимость если
признаки
делимости «
пр: числа 9, 18, 27, 36 … кратны 9 числа 1, 3, 9 являются делителями 9 НОД - наибольший общий делитель НОК - наименьшее общее кратное пр: найти НОД и НОК чисел 168 и 180 Разложим на простые делители числа 168 и 180:
Выпишем все множители в строчку: 168 = 2 · 2 · 2 · 3 · 7 180 = 2 · 2 · 3 · 3 · 5 Разложение на простые множители позволяет увидеть «состав» числа - на что оно делится. Число делится на свои простые множители и на их произведения (т.е. на числа, «составленные» из этих множителей). НОД(168; 180) - это наибольшее число, на которое делятся оба числа - и 168, и 180. НОД составляется из тех множителей, которые входят в разложения обоих чисел:
НОК(168; 180) - это наименьшее число, которое делится и на 168, и на 180. НОК составляется из всех множителей, которые входят в разложения этих чисел (без повторения):
взаимно
простые числа
- не имеют общих делителей (кроме 1)
|
Основное свойство дроби
Если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, то значение дроби не изменится:
Cравнение дробей Если
знаменатели одинаковые, то чем больше
числитель, тем больше дробь пр:
Если
числители одинаковые, то чем больше
знаменатель, тем меньше дробь пр:
Если дроби имеют разные знаменатели (и числители), то их нужно сначала привести к общему знаменателю (или числителю) Полезно помнить, что правильные дроби (<1) всегда меньше неправильных (>1) Сложение и вычитание дробей
пр:
Если знаменатели разные, то дроби нужно сначала привести к общему знаменателю Приведение дробей к общему знаменателю дроби можно «привести к общему знаменателю» домножением на «дополнительные множители»
пр:
желательно подобрать наименьшие дополнительные множители: пр:
пр:
в сложных случаях полезно разложить знаменатели на множители (чтобы увидеть общие и дополнительные): пр:
наименьшие дополнительные множители - взаимно простые числа (тогда общий знаменатель - это НОК знаменателей) |
|||||||||||||||||||||||||||||||||||||||||
|
Умножение и деление дробей
перед умножением можно (и нужно) сократить: пр:
пр:
|
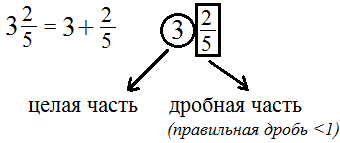
Смешанные дроби
перевод смешанной дроби в простую: к числителю прибавить целую часть, умноженную на знаменатель пр:
перевод простой дроби в смешанную: выполнить деление с остатком, остаток записать в числитель пр:
сложение: отдельно складывать целые и дробные части пр:
если получится неправильная дробь, выделить из нее целую часть пр:
…
вычитание: отдельно вычитать целые и дробные части
пр:
если вычитаемая дробь больше, то из целой части «занять 1» пр:
…
умножение и деление: перевести смешанные дроби в простые пр:
или представить смешанную дробь в виде суммы пр:
|
|||||||||||||||||||||||||||||||||||||||||
|
целые числа можно записать в виде дроби со знаменателем 1: пр:
пр:
пр:
|
||||||||||||||||||||||||||||||||||||||||||
|
Задачи на части Чтобы найти часть от числа, нужно умножить это число на соответствующую дробь.
пр:
найти
пр:
найти число,
пр: какую часть от числа 100 составляет число 15?
дополнительные дроби - в сумме дают 1 пр:
пр:
кот съел
|
||||||||||||||||||||||||||||||||||||||||||
|
Задачи на совместную работу работа
= производительность
производительность
~ «скорость
работника»
пр: труба заполняет 2 бассейна на 5 мин
Если в задаче не уточняется, какая работа выполняется, то работа принимается за 1 пр: работник выполняет какую-то работу на 5 мин
При
совместной работе производительности
складываются
Если
один работник выполняет работу за
время
|
||||||||||||||||||||||||||||||||||||||||||
Математика - 6 класс
|
Отрицательные числа пр: отрицательное число «-5» противоположно положительному числу «+5»
противоположные числа расположены по разные стороны от 0, но имеют одинаковую «абсолютную величину» - модуль
противоположные числа «по модулю» равны если к одному числу относятся два знака:
действия с отрицательными числами: - упростить запись (если несколько знаков относятся к одному числу) - определить знак результата - найти его «абсолютную величину» пр:
пр:
пр:
пр:
сравнение:
больше то число, которое находится
на оси правее пр:
запись действий с отрицательными числами: пр:
расставляем порядок действий
остались знаки «-», не занятые под действия, они относятся к отрицательным числам; при выполнении действий, сначала записываем знак результата, потом вычисляем его абсолютную величину (действие записывается «в строчку», а ниже столбик с положительными числами) 1)
|
Десятичные дроби обыкновенная дробь − запись числа в виде
десятичная дробь − запись числа в десятичной системе с дробной частью после запятой пр:
примеры действий с десятичными дробями:
пр:
перевод обыкновенной дроби в десятичную: привести знаменатель дроби к круглому числу пр:
или разделить числитель на знаменатель «столбиком», получится конечная или бесконечная периодическая десятичная дробь
перевод десятичной дроби в обыкновенную: знаменатель определяется количеством цифр после запятой пр:
способ для периодических дробей: пр:
|
|||||||||||||||
|
округление: подчеркиваем
цифру в разряде, до которого округляем;
если справа стоит цифра
пр: округлить 195,(81)
приближенные вычисления: округляем все числа до заданной точности; выполняем действие; результат округляем иррациональные числа - числа, которые невозможно представить в виде обыкновенной дроби (это бесконечные непериодические десятичные дроби) пр:
число “пи”
длина
окружности:
площадь
круга:
|
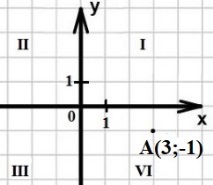
координатная ось - это прямая, на которой заданы: начало отсчета (точка 0), направление отсчета, единичный отрезок (масштаб)
расстояние между точками равно разнице между координатами правой и левой точки пр:
координатная плоскость состоит из двух координатных осей, расположенных под прямым углом, с общим началом отсчета
|
|||||||||||||||
|
Отношения отношение - это результат деления одной величины на другую, используется для сравнения величин (во сколько раз одна величина больше или меньше другой) пр: отношение двух величин
пр: разделить отрезок в отношении 2 : 3 : 1 разделим отрезок на 2+3+1=6 частей
и распределим их на три «порции» - из 2 частей, из 3 частей, из 1 части
получим
пр: разделить число 450 в отношении 4 : 5 обозначим
за x
одну часть; нужно разделить число 450
на две «порции» - из 4 частей
|
Пропорциональность пропорция
- это равенство вида
свойство
пропорции:
Две величины прямо пропорциональны, если при увеличении одной величины, вторая величина увеличивается во столько же раз. пр: на 6 м забора нужно 3 банки краски, сколько краски нужно на 5 м забора?
составим пропорцию (прямую):
Две величины обратно пропорциональны, если при увеличении одной величины, вторая величина уменьшается во столько же раз. пр: 6 рабочих покрасят забор за 3 ч, за сколько часов покрасят забор 5 рабочих?
составим пропорцию (обратную):
|
|
Буквенные выражения Знак
умножения « пр:
упрощение выражений: - раскрытие скобок
- приведение подобных слагаемых (группировка) пр:
пр:
составление выражений и уравнений: «запись на математическом языке»
|
схема решения уравнений: «избавляемся» от дробей (умножаем уравнение на общий знаменатель) пр:
раскрываем скобки пр:
слагаемые, содержащие «неизвестную», переносим налево, все остальное - направо пр:
«приводим подобные слагаемые» пр:
делим уравнение на «коэффициент при неизвестной» пр:
можно сделать проверку - подставить найденный корень в уравнение и проверить, получилось ли верное равенство пр:
Уравнение может не иметь корней или иметь бесконечно много корней: пр:
пр:
|
||||||||||||||||||||||||||
|
Уравнения Уравнение - это равенство, содержащее неизвестную величину, значение которой нужно найти. Корень уравнения - это значение «неизвестной», при котором из уравнения получается верное равенство. Решить уравнение - значит, найти все его корни (или убедиться, что корней нет). простые уравнения:
свойства уравнений: - левую и правую части уравнения можно увеличить или уменьшить на одно число пр:
т.е. «слагаемое» можно перенести из одной части уравнения в другую, изменив знак на противоположный - левую и правую части уравнения можно умножить или разделить на одно число пр:
чтобы
решить уравнение, нужно привести его
к виду:
|
|
Проценты |
|||||||||||
|
1% какой-либо величины – это одна сотая часть этой величины, т.е. задачи на проценты - это задачи на части 1%
от A =
100%
от A
проценты принято записывать в виде десятичных дробей пр:
|
увеличить
на p%
- взять
уменьшить
на p%
- взять
пр:
пр: Товар стоил 300 р, потом цена повысилась на 10%, потом понизилась на 10%. Сколько теперь стоит товар? увеличить
на 10%
уменьшить
на 10%
|
||||||||||
|
Задачи на проценты |
|||||||||||
|
найти процент от числа |
найти число по его проценту |
найти процентное соотношение |
|||||||||
|
пр: найти 14% от числа 150 |
пр: найти число, 14% которого равны 21 |
пр: сколько процентов от 150 составляет число 21? |
|||||||||
|
1
способ
- по формуле
где p - процент (дробь), A - целая величина, Q - часть этой величины |
|||||||||||
|
|
|
|
|||||||||
|
2 способ - найти сначала 1% |
|||||||||||
|
|
|
|
|||||||||
|
3 способ - составить пропорцию |
|||||||||||
|
|
|
|
|||||||||
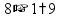
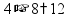
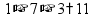
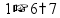
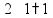
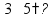
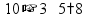
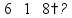
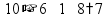
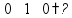
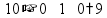
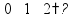
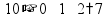
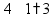
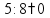

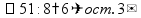
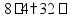
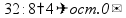
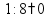
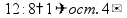
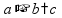
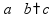
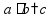
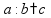
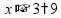
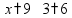
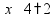
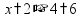
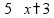
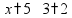
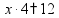
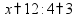
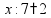
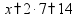
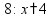
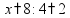
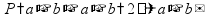
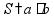
 1000
=
1000
=
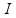
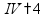
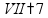
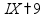
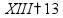
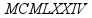
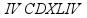
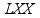
 365/366 сут
365/366 сут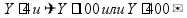

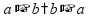
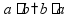
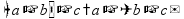
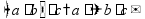
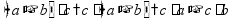
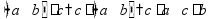
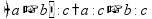
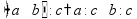
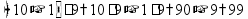
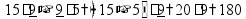
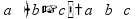
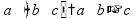
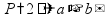
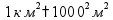
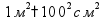
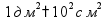
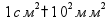
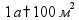
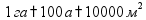
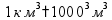
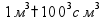
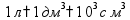
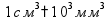
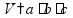
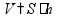
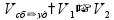
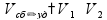
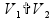 )
)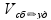 –
– 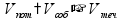
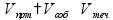
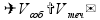
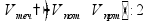
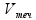 –
– 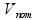 –
– 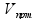 –
– 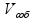 –
–
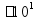
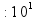
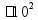
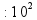
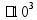
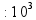
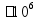
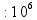
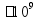
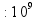
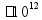
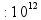
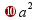
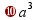






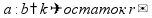 ,
то
,
то
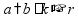
 »
означает «делится на»
»
означает «делится на»
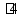
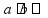

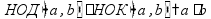
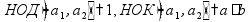
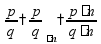
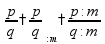
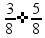
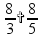
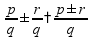
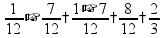
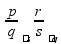
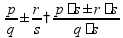
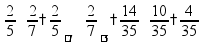
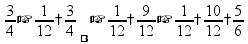
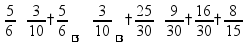
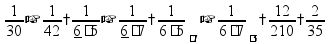
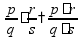
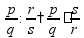
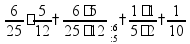
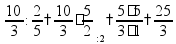
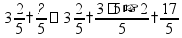
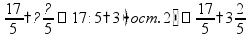
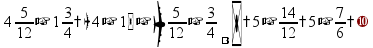
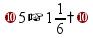
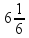
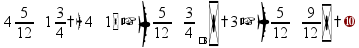
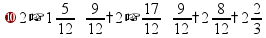
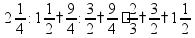
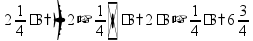
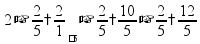
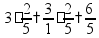

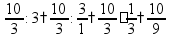
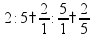
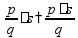
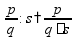
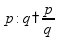
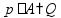
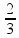 от 12
от 12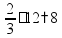
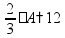
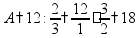
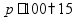
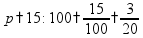
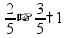
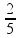
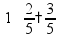
 время
время
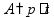
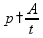
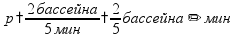
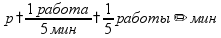
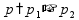
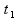 ,
другой - за время
,
другой - за время
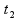 ,
а вместе они выполнят эту работу за
время
,
а вместе они выполнят эту работу за
время
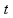
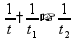
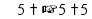
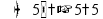
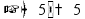
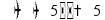
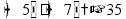
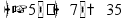
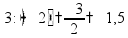
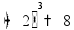
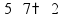
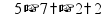
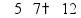
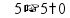
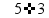
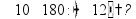
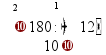
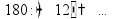
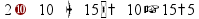
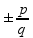
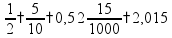
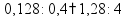

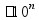
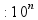
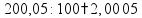
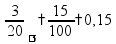
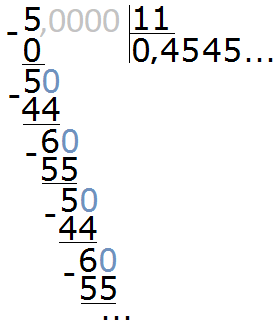
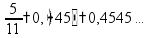
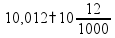
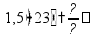 пусть
пусть
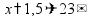 ,
тогда
,
тогда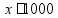 ,
а
,
а 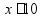 ;
вычтем из первого второе
;
вычтем из первого второе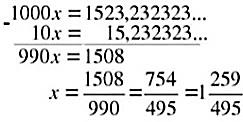
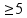 ,
то подчеркнутую цифру увеличиваем на
1
,
то подчеркнутую цифру увеличиваем на
1 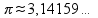 (это отношение длины окружности к ее
диаметру - одинаково для всех окружностей)
(это отношение длины окружности к ее
диаметру - одинаково для всех окружностей)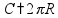
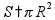
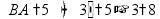
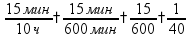
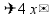 и
из 5 частей
и
из 5 частей
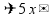
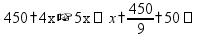
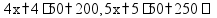
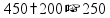
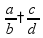
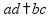
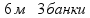
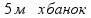
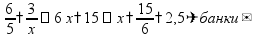
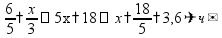
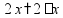
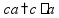
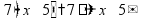
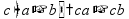
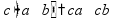
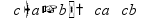
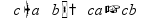
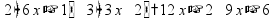
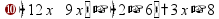
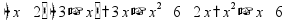
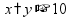
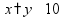
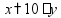
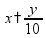
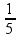 от
y
от
y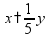
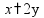
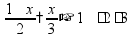
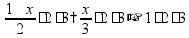
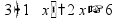
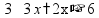
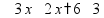
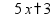
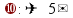
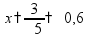
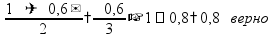
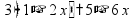
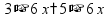
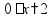
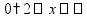
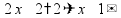
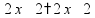
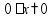
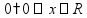
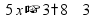
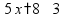
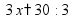
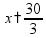
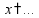
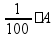 p% от A
p% от A
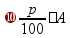
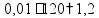
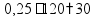
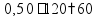
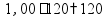
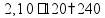
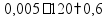
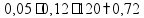
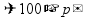
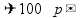
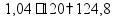
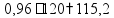
 умножить на 1,1
умножить на 1,1 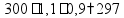 (р)
(р)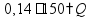
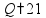
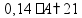
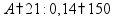
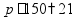
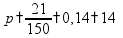
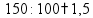 (1%)
(1%)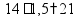 (14%)
(14%)