Алгебра - 10 класс
|
Рациональные уравнения распадающиеся уравнения
Рациональные неравенства метод интерваловдля неравенств вида
пр:
четные
точки:
нечетные
точки:
выражение меняет знак только в нечетных точках - отмечаем на оси точки перемены знака, изображаем дугами промежутки знакопостоянства - если неравенство нестрогое, то точки из числителя закрасим (в этих точках выражение равно нулю), а точки из знаменателя оставим незакрашенными (знаменатель не должен быть равен нулю, в этих точках выражение не определено) - на самом правом промежутке выражение положительно - «идем» справа налево через точки перемены знака: в «четных» точках знак остается прежним, в «нечетных» точках знак меняется на противоположный - записываем ответ в соответствии со знаком исходного неравенства (включая закрашенные точки и исключая незакрашенные) пр:
если неравенство имеет не совсем подходящий вид, то его нужно преобразовать: пр: разделим
нер-во на
«перевернем»
скобку (т.е. умножим нер-во на
«вынесем» 5 за скобку
теперь можно применить метод интервалов
|
Система
(уравнений или неравенств)
пр:
Совокупность
(уравнений или неравенств)
пр:
|
|||||||||||
|
Метод замены неизвестных пр:
замена
пр:
|
||||||||||||
|
|
||||||||||||
|
Функция
пр:
пр:
|
Функция (
Показательные уравнения и неравенства
пр:
метод приведения к одному основанию: пр:
пр: (если основание <1, при «отбрасывании оснований» знак неравенства меняется) |
|||||||||||
|
Функция (
Логарифмические уравнения и неравенства
пр:
пр: (если основание <1, то знак неравенства меняется) метод приведения к одному основанию: пр:
пр: пр:
ОДЗ:
|
||||||||||||
|
Логарифмы
(основное логарифмическое тождество) a - «основание логарифма» b - «выражение под логарифмом» пр:
свойства логарифмов:
специальные обозначения:
пр:
|
||||||||||||
|
Тригонометрия
|
радиан - величина угла, соответствующего дуге окружности, длина которой равна радиусу (не зависит от окружности) синус (sin), косинус (cos), тангенс (tg), котангенс (ctg) (угла на единичной окружности)- это координаты соответствующего радиус-вектора по осям синусов (x=0), косинусов (y=0), тангенсов (x=1), котангенсов (y=1)
(не
опред.при
(не
опред.при
|
|||||||||||
|
Тригонометрические функции
|
Обратные тригонометрические функции
|
|||||||||||
|
Тригонометрические уравнения
или
|
|||||||||||
|
Тригонометрические формулы
|
||||||||||||


 где
где - точки перемены знака -
«четные»
и «нечетные»
- точки перемены знака -
«четные»
и «нечетные»
 (т.к. эта скобочка входит в выражение
в четной степени)
(т.к. эта скобочка входит в выражение
в четной степени)


 (при умножении или делении на
отрицательное число знак нер-ва
меняется)
(при умножении или делении на
отрицательное число знак нер-ва
меняется)
 )
)



 пересечение
решений
пересечение
решений





 замена
замена


 (степенная)
(степенная)













 (показательная)
(показательная) )
)
 (
( )
)
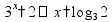



 (логарифмическая)
(логарифмическая)
 (
(









 -
«степень, в которую нужно возвести a,
чтобы получить b»
-
«степень, в которую нужно возвести a,
чтобы получить b»








 (переход
к другому основанию)
(переход
к другому основанию)
 (десятичный
логарифм)
(десятичный
логарифм) (натуральный
логарифм,
(натуральный
логарифм,
 )
) (
( стандартный
вид числа)
стандартный
вид числа)




 )
)
 )
)
 -
четная, период
-
четная, период


 - нечетная, период
- нечетная, период

 и
и -
нечетные, период
-
нечетные, период







































 ,
,

























