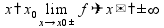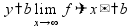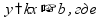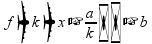Алгебра - 11 класс
|
Производная |
||||||||||||||||||||||||||||||||||||||||||||||
геометрический
смысл: тангенс
угла наклона касательной физический смысл: скорость изменения функции
пр:
скорость - производная от координаты по времени, ускорение - производная от скорости по времени |
производная (функция): функция, которая в каждой точке равна значению производной от «первообразной» функциив этой точке дифференцирование- нахождение производной правила дифференцирования: можно пользоваться таблицей производных
пр:
уравнение
касательнойк
функции
приближенные вычисления
пр:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Интеграл |
||||||||||||||||||||||||||||||||||||||||||||||
интегрирование - нахождение функции (первообразной) по ее производной правила интегрирования: можно пользоваться таблицей интегралов
пр:
пр:
пр: формула интегрирования по частям:
пр:
|
определенный интеграл (формула Ньютона-
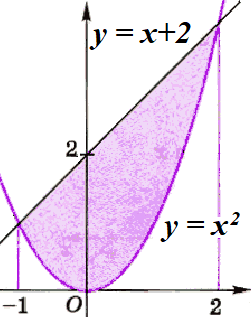
площадь фигуры между графиками функций:
если
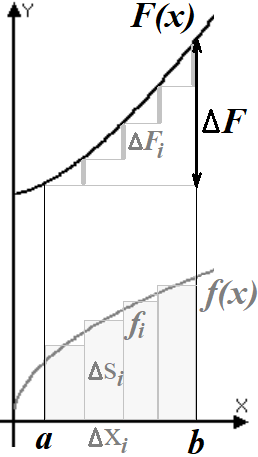
физический смысл интеграла:сумма
пр:
перемещение - интеграл от скорости, работа - интеграл от силы свойства определенного интеграла:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
таблица производных и интегралов
|
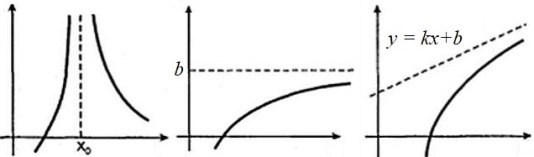
предел
функции
в точке (или на бесконечности) -
величина,
к которой стремится значение функции,
когда аргумент стремится к этой точке
(слева или справа)
пр: «замечательные» пределы:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Равносильностьуравнений и неравенств |
||||||||||||||||||||||||||||||||||||||||||||||
|
с модулем
распадающиеся, дробные
сокращение
|
иррациональные
показательные
логарифмические
равносильные уравнения/неравенства/системы - имеют одинаковые множества корней использование формул (свойств корней, логарифмов, тригонометрических функций) может привести к неравносильным преобразованиям |
|||||||||||||||||||||||||||||||||||||||||||||
|
Исследование функций
точка
пересечения с осью y:
точки
пересечения с осью x:
нахождение минимума/максимума функции: сравнить значения функции в критических точках и на границах области определения, в точках разрыва
|
||||||||||||||||||||||||||||||||||||||||||||||
|
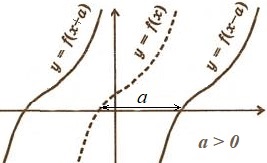
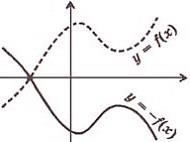
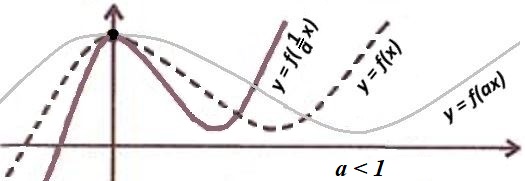
Преобразования графиков функций
|
||||||||||||||||||||||||||||||||||||||||||||||
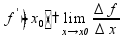


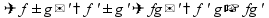


 в
точке
в
точке


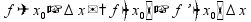
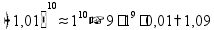

 -
первообразная для функции
-
первообразная для функции

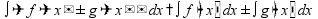

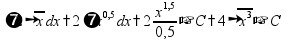
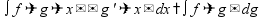


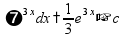
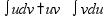


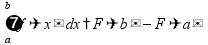
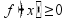 на
на
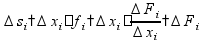

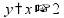

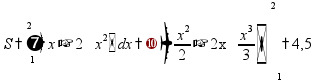
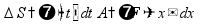

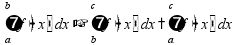
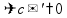


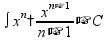











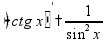


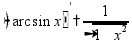



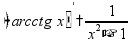
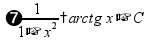


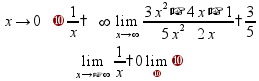

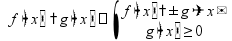



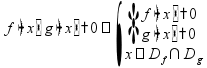

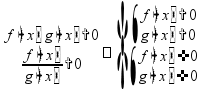






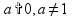




 -
значения аргумента, для которых
функция определена (выражение имеет
смысл)
-
значения аргумента, для которых
функция определена (выражение имеет
смысл)

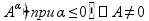


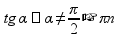

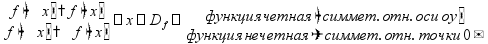

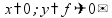
 (нули
функции)
(нули
функции)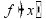 не
опр. или имеет разрыв пр:
не
опр. или имеет разрыв пр:
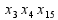
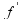 не
опр.
не
опр.

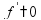
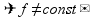

 меняет знак
меняет знак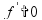

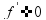

 не
опр.или
не
опр.или


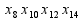




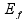 -
множество
значений, которые может принимать
функция
-
множество
значений, которые может принимать
функция